آموزش کامل و جامع تبدیل لاپلاس و نحوه محاسبه آن همراه با مثال

این جزوه بهعنوان یک راهنمای خودآموز برای دانشجویانی طراحی شده است که تازه با تبدیل لاپلاس آشنا شدهاند. ما از مفاهیم پایه شروع خواهیم کرد و فرض میکنیم که شما دانشی در زمینه حساب دیفرانسیل و انتگرال (انتگرالها، مشتقها و حدها) و اعداد مختلط دارید. اگر با اعداد مختلط آشنا نیستید، آنها را بهصورت مختصر مرور خواهیم کرد، همچنین میتوانید از جزوات و فیلمهای آموزشی مرتبط با اعداد مختلط که در مقاله اختصاصی منتشرشده در سایت آلفا مث با عنوان بررسی کامل درس ریاضی عمومی 1 نیز موجود است؛ برای کسب اطلاعات درباره اعداد مختلط استفاده نمایید. مثالها از ساده به پیچیده پیش خواهند رفت و درک شما را گام به گام تقویت خواهند کرد. در پایان، یک جدول از تبدیلهای لاپلاس رایج و جدولی جداگانه برای ویژگیهای کلیدی برای ارجاع سریع ارائه خواهیم داد. در نهایت، این مفاهیم را برای حل معادلات دیفرانسیل به کار خواهیم برد.
فهرست محتوا
Toggle۱. مرور اعداد مختلط
قبل از پرداختن به تبدیل لاپلاس، بیایید بهسرعت اعداد مختلط را مرور کنیم، زیرا این اعداد در دامنه تبدیل لاپلاس ظاهر میشوند.
یک عدد مختلط در فرم دکارتی بهصورت زیر است:
– : بخش حقیقی
– : بخش موهومی
– (در نماد مهندسی؛ ریاضیدانان معمولاً از
استفاده میکنند)
در فرم قطبی:
– : اندازه یا ماژول،
– : زاویه یا فاز،
– فرمول اویلر:
نمایی مختلط:
مثال (ساده): محاسبه کنید .
مثال (متوسط): اندازه را بیابید.
این مفاهیم را در تبدیل لاپلاس استفاده خواهیم کرد، جایی که (بخش حقیقی
، بخش موهومی
).
۲. مقدمهای بر تبدیلهای انتگرالی
تبدیلهای انتگرالی ابزارهایی هستند که مسائل شامل مشتقگیری را به مسائل جبری تبدیل میکنند و حل آنها را آسانتر میکنند.
یک تبدیل انتگرالی بهصورت زیر است:
– : تابع ورودی (مثلاً در دامنه زمان)
– : هسته
– : تابع تبدیلشده
این امکان را فراهم میکند که معادلات دیفرانسیل را بهصورت جبری در دامنه حل کنیم و سپس به دامنه
بازگردیم.
تبدیلهای انتگرالی رایج:
– تبدیل فوریه:
– تبدیل لاپلاس: (موضوع این راهنما)
تبدیل لاپلاس برای سیگنالهایی که از شروع میشوند، مفید است و در مهندسی (مثلاً سیستمهای کنترل) رایج است.
۳. مرور انتگرالهای ناسره
تبدیلهای لاپلاس شامل انتگرالهای ناسره در دامنههای نامتناهی هستند.
یک انتگرال ناسره بهصورت زیر است:
– اگر حد وجود داشته باشد، همگرا است؛ در غیر این صورت، واگرا است.
مثال (ساده): ،
ثابت.
– برای همگرا است؛ برای
واگرا است.
مثال (متوسط): برای
.
(واگرا).
این موارد را تمرین کنید تا همگرایی در تبدیلهای لاپلاس را درک کنید.
۴. تعریف تبدیل لاپلاس
فرض کنید برای
تعریف شده باشد، با
برای
.
تبدیل لاپلاس تابع بهصورت زیر است:
– : متغیر مختلط (
)
– دامنه: مقادیر که انتگرال در آنها همگرا است.
نمادگذاری: ، با استفاده از حروف بزرگ برای تبدیلها (مثلاً
).
اگر تکانههایی در وجود داشته باشد، آنها را در نظر میگیریم:
.
۵. وجود تبدیل لاپلاس
برای وجود :
1. در بازه
برای هر
محدود، بهصورت تکهای پیوسته باشد.
– تکهای پیوسته: زیربازههای محدود که در آنها پیوسته است، با حدهای محدود در نقاط انتهایی.
2. از مرتبه نمایی باشد:
برای
، با
،
،
.
3. محور همگرایی: بهگونهای که
برای
.
قضیه: اگر شرایط ۱ و ۲ برقرار باشند، برای
وجود دارد.
مثالها:
– : از مرتبه نمایی با
،
،
.
– : از مرتبه نمایی با
،
،
(از قاعده لوپیتال دو بار استفاده کنید:
).
– : از مرتبه نمایی نیست.
همچنین، برای
، و برای
بهصورت تکهای پیوسته است.
۶. خطی بودن تبدیل لاپلاس
تبدیل لاپلاس خطی است.
قضیه: اگر برای
و
برای
، آنگاه برای ثابتهای
:
اثبات: از خطی بودن انتگرالها ناشی میشود.
مثال: در مثال ۵ زیر استفاده شده است.
همچنین درس بهینهسازی خطی یکی از مباحث کلیدی و کاربردی در رشتههای مهندسی، ریاضیات، مدیریت و علوم داده است. این درس به بررسی روشها و الگوریتمهایی میپردازد که با استفاده از آنها میتوان بهترین تصمیم را در شرایط محدودیت منابع اتخاذ کرد. مفاهیمی مانند برنامهریزی خطی، روش سیمپلکس، دوگانسازی و تحلیل حساسیت از محورهای اصلی این درس به شمار میآیند. برای آشنایی کامل با سرفصلها، کاربردها و اهمیت این مبحث در دنیای واقعی، پیشنهاد میشود مقاله «درس بهینهسازی خطی» را در سایت آلفا مث مطالعه کنید. این مطلب دیدی جامع و دقیق نسبت به ساختار و کارکرد این درس در حوزههای مختلف ارائه میدهد.
۷. مثالهای پایهای از تبدیلهای لاپلاس
ما از موارد ساده شروع میکنیم و به پیچیدگی بیشتر میرسیم.
مثال ۱ (ساده: ثابت): (
).
مثال ۲ (ساده: نمایی): .
مثال ۳ (متوسط: نمایی مختلط): .
مثال ۴ (متوسط: سینوس): .
با استفاده از خطی بودن، تبدیل لاپلاس بهصورت زیر است:
مثال ۵ (متوسط: ترکیب خطی): .
مثال ۶: فرض کنید ،
. تبدیل لاپلاس بهصورت زیر است:
با انتگرالگیری جزء به جزء داریم:
بهطور مشابه:
بنابراین:
مثال ۷: تابع تکهای پیوسته را تعریف کنید:
تبدیل لاپلاس بهصورت زیر است:
مثال ۸ (تکانه): (دلتا دیراک).
مثال ۹ (تکانه مرتبه بالاتر): .
مثال ۱۰ (توانهای ):
(
).
برای محاسبه، از انتگرالگیری جزء به جزء استفاده میکنیم:
با ،
،
،
:
که برای صادق است.
با اعمال بازگشتی این فرمول، داریم:
مثال ۱۱ (پالس مستطیلی): برای
، در غیر این صورت ۰ (
).
مثال ۱۲: فرض کنید ،
. تبدیل لاپلاس بهصورت زیر است:
قضیه (قضیه جابجایی نمایی):
اگر برای
وجود داشته باشد و
ثابت باشد، آنگاه:
اثبات: این نتیجه مستقیماً از تعریف بهدست میآید:
که برای صادق است.
۸. جدول کوتاه تبدیلهای لاپلاس رایج
برای ارجاع سریع:
از این جدول برای تبدیلهای مستقیم و معکوس استفاده کنید.
همچنین رشته ریاضیات یکی از بنیادیترین و تأثیرگذارترین حوزههای علمی است که نقش مهمی در پیشرفت فناوری، علوم مهندسی، اقتصاد و حتی علوم انسانی ایفا میکند. این رشته فراتر از محاسبات و معادلات ساده است و بستری برای پرورش تفکر تحلیلی، استدلال منطقی و حل مسائل پیچیده فراهم میآورد. اگر قصد دارید با ساختار این رشته، دروس تخصصی، گرایشهای مختلف و فرصتهای شغلی آن آشنا شوید، توصیه میشود مقاله «صفرتاصد رشته ریاضیات و کاربردها» را مطالعه کنید. این مطلب راهنمایی جامع برای علاقهمندان و داوطلبان ورود به این حوزه علمی محسوب میشود.
۹. ویژگیهای تبدیل لاپلاس
ویژگیهای کلیدی در جدول زیر برای ارجاع آسان خلاصه شدهاند. هر یک شامل توضیح مختصر و مثال است.
ویژگی یکبهیک: اگر ، آنگاه
(تقریباً؛ فقط در نقاط محدود بدون تکانه متفاوت است).
9.1 مقیاسبندی زمانی
سیگنال را بهصورت
تعریف کنید، که در آن
. آنگاه:
منطقی است: زمانها به اندازه مقیاس میشوند، فرکانسها به اندازه
.
بیایید بررسی کنیم:
که در آن .
مثال: ، بنابراین:
9.2 مقیاسبندی نمایی
فرض کنید یک سیگنال و
یک اسکالر باشد، و
را تعریف کنید. آنگاه:
بیایید بررسی کنیم:
مثال: ، و بنابراین:
9.3 تبدیل لاپلاس مشتقها
قضیه (تبدیل لاپلاس مشتقها):
فرض کنید پیوسته باشد و
در هر بازه
بهصورت تکهای پیوسته باشد. فرض کنید
و
از مرتبه نمایی باشند با
برای برخی ثابتهای
و
و
. آنگاه
برای
وجود دارد و بهصورت زیر است:
طرح اثبات: اگر پیوسته بود، آنگاه بررسی کنید:
که صرفاً از انتگرالگیری جزء به جزء استفاده میکند.
ادامه طرح اثبات: از قبل داشتیم:
وقتی و با استفاده از مرتبه نمایی
و
، این عبارت بهصورت زیر میشود:
برای تکمیل اثبات عمومی با تکهای پیوسته، انتگرال را به زیربازههایی تقسیم میکنیم که در آنها
پیوسته است.
هر یک از این انتگرالها با انتگرالگیری جزء به جزء محاسبه میشود، سپس پیوستگی باعث جمع شدن ارزیابیهای نقاط انتهایی میشود و امکان استفاده از انتگرال منفرد سمت راست را فراهم میکند، که اثبات عمومی را تکمیل میکند.
نتیجه (تبدیل لاپلاس مشتقها):
فرض کنید:
1. توابع پیوسته باشند و
در هر بازه
بهصورت تکهای پیوسته باشد.
2. توابع از مرتبه نمایی باشند با
برای برخی ثابتهای
و
و
.
آنگاه برای
وجود دارد و بهصورت زیر است:
برای معادلات دیفرانسیل مرتبه دوم، معمولاً از این استفاده میکنیم:
مثال: فرض کنید با:
اگر ، آنگاه:
با:
قضیه مشتق ما میدهد:
اما:
9.4 انتگرال
فرض کنید انتگرال تجمعی سیگنال
باشد، یعنی:
آنگاه:
یعنی انتگرال در دامنه زمان به تقسیم بر متغیر فرکانس تبدیل میشود.
مثال: ، بنابراین
.
تابع پله واحد است:
9.5 ضرب در 
فرض کنید یک سیگنال باشد و تعریف کنیم:
آنگاه:
برای تأیید فرمول، کافی است دو طرف معادله زیر را مشتق بگیریم:
نسبت به :
مثالها:
– ،
:
– ،
:
– بهطور کلی:
9.6 تکانهها در 
اگر شامل تکانههایی در
باشد، ما انتخاب میکنیم که آنها را در انتگرال تعریفکننده
لحاظ کنیم:
(میتوانید انتخاب کنید که آنها را شامل نکنید، اما این کار برخی فرمولهایی که خواهیم دید و استفاده میکنیم را تغییر میدهد)
مثال: تابع تکانه، :
F(s) = \int_{0^-}^\infty \delta(t) e^{-s t} \, dt = e^{-s t} \bigg|_{t=0} = 1
بهطور مشابه برای :
قضیه:
فرض کنید (۱) در هر بازه
بهصورت تکهای پیوسته باشد، و (۲) از مرتبه نمایی با توان
باشد. آنگاه برای هر عدد صحیح مثبت:
اثبات:
نتیجه: برای هر عدد صحیح، :
9.7 کانولوشن
کانولوشن سیگنالهای و
، که با
نشان داده میشود، سیگنال زیر است:
– برابر است با . به عبارت دیگر،
.
– اهمیت بسیار زیاد آن بهزودی روشن خواهد شد.
از نظر تبدیل لاپلاس:
تبدیل لاپلاس، کانولوشن را به ضرب تبدیل میکند.
بیایید نشان دهیم که :
که در آن روی مثلث انتگرال میگیریم.
– تغییر ترتیب انتگرالگیری:
– تغییر متغیر به
.
. ناحیه انتگرالگیری به
،
تبدیل میشود:
۱۰. تبدیل لاپلاس معکوس
تبدیل معکوس، را از
بازیابی میکند:
– (محور همگرایی).
– در عمل، به جای این انتگرال از جدولها، کسرهای جزئی یا ویژگیها استفاده کنید.
تبدیل یکبهیک است، بنابراین معکوس بهخوبی تعریف شده است.
مثال (ساده): .
مثال (متوسط): .
۱۱. گسترش کسرهای جزئی برای تبدیلهای معکوس
برای کسری (
)، به کسرهای جزئی گسترش دهید.
فرض کنید قطبهای ساده: .
باقیمانده: .
آنگاه: .
مثال: تبدیل لاپلاس معکوس را بیابید:
گسترش کسرهای جزئی بهصورت زیر است:
بنابراین:
برای قطبهای تکراری یا کسرهای درجه دوم، تنظیم کنید (مثلاً ).
۱۲. حل معادلات دیفرانسیل خطی با تبدیل لاپلاس
تبدیل لاپلاس معادلات دیفرانسیل معمولی (ODE) را به معادلات جبری تبدیل میکند.
مراحل:
1. تبدیل لاپلاس هر دو طرف معادله را بگیرید.
2. از ویژگی مشتق برای شرایط اولیه استفاده کنید.
3. برای حل کنید.
4. با استفاده از کسرهای جزئی/جدولها، تبدیل معکوس بگیرید.
مثال (ساده: مرتبه اول): ،
.
.
مثال: مسئله مقدار اولیه زیر را در نظر بگیرید:
با گرفتن تبدیل لاپلاس، داریم:
با ، قضایای مشتق ما میدهند:
یا:
میتوانیم بنویسیم:
یک نتیجه مهم از قضیه اساسی جبر، تجزیه کسرهای جزئی است.
ما مینویسیم:
بهطور معادل:
با قرار دادن ، داریم
یا
.
ضریب میدهد
، بنابراین
.
ضریب میدهد
، بنابراین
.
از تجزیه کسرهای جزئی با ،
، و
:
بهطور معادل، میتوانیم این را بنویسیم:
اما، ،
، و
، بنابراین تبدیل لاپلاس معکوس میدهد:
که مسئله مقدار اولیه را حل میکند.
مثال (جرم-فنر-دمپر):
معادلات حرکت برای سیستم بهصورت زیر هستند:
تبدیل لاپلاس معادله بهصورت زیر میشود:
حل معادله برای و تجزیه آن به کسرهای جزئی، بهدست میآید:
بنابراین، تبدیل لاپلاس معکوس بهصورت زیر میشود:
سرعت جرم میتواند بهصورت زیر محاسبه شود:
مثال بررسی مشتق: ،
.
–
– ، که با محاسبه مستقیم مطابقت دارد.
۱۳. موضوعات اضافی: کانولوشن و بیشتر
کانولوشن: .
.
مثال: کانولوشن با تکانه: ،
.
مثال: انتگرال بهعنوان کانولوشن با پله: ،
.
کاربران گرامی سایت آلفا مث میتوانند تا از دیگر مطالب اختصاصی منتشرشده در سایت آلفا مث در ارتباط با موضوعات تخصصی مرتبط با دروس و مطالب ریاضیات در سطح دانشگاهی که در دسته بندی ریاضیات دانشگاهی موجود است نیز استفاده نمایند.

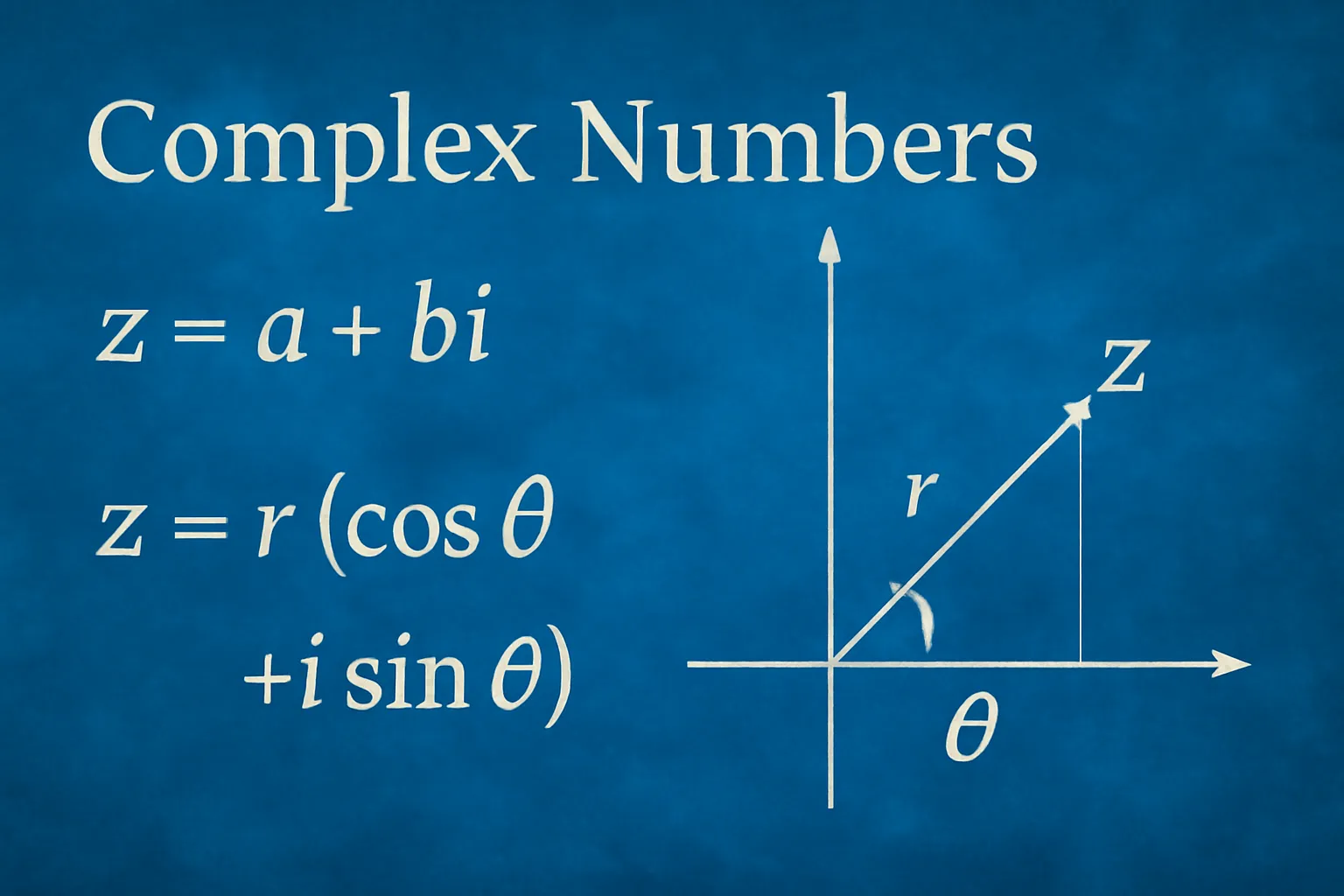

![Rendered by QuickLaTeX.com \[f(t) = \begin{cases} e^{2 t}, & 0 \leq t < 1, \\ 4, & 1 \leq t. \end{cases}\]](https://alphaamath.com/wp-content/ql-cache/quicklatex.com-0b60d90aabbd7bde686c0f4b6753edb5_l3.png)
![Rendered by QuickLaTeX.com \mathcal{L}[1] = \int_{0}^{\infty} e^{-s t} \, dt = -\lim_{A \to \infty} \frac{e^{-s t}}{s} \bigg|_{0}^{A} = -\lim_{A \to \infty} \left( \frac{e^{-s A}}{s} - \frac{1}{s} \right) = \frac{1}{s}, \quad \Re\{s\} > 0.](https://alphaamath.com/wp-content/ql-cache/quicklatex.com-1b2750e36d55740a5798801bf95bc7a7_l3.png)





دیدگاهتان را بنویسید